Fesselballons, arithmetische und geometrische Reihen
In der Technik muss man öfter einmal Dinge vergrößern oder verkleinern. Der Fachausdruck dafür nennt sich Skalieren. Auf diese Weise kann man auch einen im Prinzip gleichen Gegenstand, wie etwa eine Schraube, in verschiedenen Größen herstellen. Um in so einem Fall eine vernünftige Abstufung der Größen zu erreichen, kann man Normzahlen verwenden. Die Reihen der Normzahlen nennt man auch Renard-Serien.
Normzahlen blühen im Verborgenen
Leute, die nichts mit der Konstruktion von Maschinen und Maschinenelementen zu tun haben, können ihr ganzes Leben verbringen, ohne jemals mit dem Begriff der Normzahlen konfrontiert zu werden. Und doch beeinflussen wir unser Leben. Man könnte sogar sagen, dass sie zu unserem Wohlstand beitragen.

Was, bitte, sollen geometrische Reihen – das sind die Normzahlreihen nämlich – mit unserem Wohlstand zu tun haben? Ganz einfach: Normzahlen vereinfachen Konstruktion und Fertigung von Dingen. Dadurch geht manches schneller und wird damit billiger. Billiger bedeutet aber wiederum, dass wir uns von unserem Geld mehr leisten können. Also mehr Wohlstand für alle. Vorausgesetzt natürlich, die Leistung unserer Wirtschaft wird gerecht verteilt. Aber das ist eine andere Geschichte…
Folgen und Reihen
Eine Folge im Sinne der Mathematik ist einfach eine Aufzählung von Zahlen. Zum Beispiel die Anzahl von Zigaretten, die einer an den verschiedenen Tagen einer Woche geraucht hat: am Sonntag 35 Stück, am Montag 38 Stück, am Dienstag 34 Stück usw. Dabei müssen die einzelnen Glieder der Folge in keinerlei definierter Beziehung zueinanderstehen.
Eine Reihe ist nun eine spezielle Folge. Hier steht jedes Glied in einer bestimmten mathematischen Beziehung zu seinem Vorgänger und seinem Nachfolger. Ein einfaches Beispiel sind die Höhen der einzelnen Auftritte einer Treppe über dem Fußboden. Wenn eine einzelne Treppenstufe 17 cm hoch ist, ist der Auftritt der ersten Stufe 17 cm über dem Fußboden, der der zweiten 34 cm, der der dritten 51 cm usw.: Jede Stufe liegt 17 cm höher über dem Beginn der Treppe als die vorhergehende.
Eine solche Reihe nennt man arithmetische Reihe. Sie ist bei manchen Anwendungen sinnvoll. Eben bei einer Treppe aber zum Beispiel auch bei Schuhgrößen. Die Zahl einer Schuhgröße ist ein Maß in der seltsamen Maßeinheit „Pariser Stich“. Ein Pariser Stich ist etwa zwei Drittel eines Zentimeters. Die Schuhgröße, die bei uns auf der Schachtel steht, bezeichnet die Länge des Leistens, also des „Fußmodells“, über den der Schuh gefertigt wurde. Jede Schuhgröße ist also 0,666 cm länger als die nächst kleinere. So ist zum Beispiel ein Schuh der Größe 36 innen etwa 24 cm lang. Damit sich der Fuß beim Abrollen bewegen kann, wählt man die Schuhgröße eineinhalb bis zwei Zentimeter länger als die Fußlänge. Ein 36er Schuh passt also jemandem, dessen Fuß 22 bis 22,5 cm lang ist.
Geometrische Reihen und Normzahlen
Bei Schuhgrößen ist es nun sinnvoll, wenn sie eine arithmetische Reihe bilden. Also jede Stufe gleich groß ist: es gibt Leute mit 22 cm langen Füßen und genauso gut Leute mit 24 cm langen Füßen. Jemand kann aber auch 28 cm lange Füße haben, so dass er Schuhgröße 45 benötigt und ein anderer benötigt Größe 46, weil sein Fuß 29 cm lang ist. Und auch bei einer Treppe ist es sinnvoll, dass die 20. Stufe genauso hoch ist wie die dritte.
Es gibt aber auch Fälle, bei denen die Abstufung bei den größeren Größen auch größer wird. So ist es sinnvoll, dass es metrische Gewinde mit 4, 5 und 6 mm Nenndurchmesser gibt: M 4, M 5 und M 6. Wenn wenn man aber in der Größenordnung von 50 mm unterwegs ist, wäre es nicht sinnvoll, wenn auf die Größe M 48 die M 49 und dann die M 50 folgen würde. Tatsächlich gibt es M 48, M 56 und M 64. Wenn eine Schraube M 5 zu schwach ist, ist es gut denkbar, dass eine mit M 6 ausreicht. Ist aber M 48 zu schwach, würde 1 mm mehr auch nicht viel ausmachen. Da ist es dann sinnvoll, wenn man gleich deutlich mehr zugibt. Und deswegen ist die nächste Größe eben M 56.
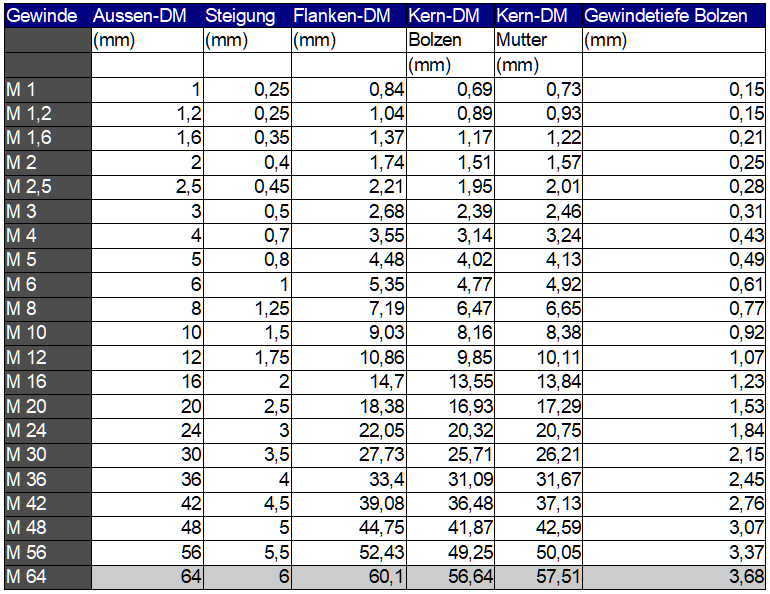
Schaut man sich die in der DIN 13 genau Durchmesser für metrische Spitzgewinde näher an, stellt man fest: Jede Größe ist ganz grob 1,2 mal so groß wie die vorhergehende. M 1,0; M 1,2; M 1,6; M 2,0; M 2,5; M 3; M 4; M 5; M 6; M 8; M 10… Natürlich hat man hier sich ergebende krumme Zahlen gerundet. Bei den ganz kleinen auf Zehntel Millimeter, dann auf halbe und schließlich auf ganze Millimeter.
Eine solche Reihe, bei der jedes Glied um einen bestimmten Faktor größer oder kleiner ist als sein Vorgänger oder Nachfolger, nennt man geometrische Reihe. Die verschiedenen Reihen von Normzahlen sind nun nichts anderes als ganz bestimmte solche geometrische Reihen.
Warum arithmetisch? Warum geometrisch?
Warum heißt nun eigentlich eine Reihe mit konstanter Stufenhöhe arithmetisch und eine mit einem Faktor geometrisch? Das hat mit den beiden Begriffen arithmetisches Mittel und geometrisches Mittel zu tun.
Das arithmetische Mittel ist das, was wir landläufig als Durchschnitt oder Mittelwert bezeichnen. Die Summe mehrerer Zahlen geteilt durch ihre Anzahl. Bei einer Treppe mit 17 cm Stufenhöhe wäre die dritte Stufe 3 × 17 cm = 51 cm hoch. Die fünfte wäre 5 × 17 cm = 85 cm hoch. Nimmt man von beiden Zahlen das arithmetische Mittel (51 cm + 85 cm)/2 = 68 cm, bekommt man die Höhe der vierten Stufe. 4 × 17 cm ist nämlich auch 68 cm. Weil bei dieser Art von Reihen jede Stufe dem arithmetischen Mittel aus ihrem Vorgänger und ihrem Nachfolger entspricht, nennt man sie arithmetische Reihen. Man spricht auch von einer arithmetischen Abstufung.

Das geometrische Mittel von zwei Zahlen entspricht der Wurzel aus dem Produkt der beiden Zahlen. Nehmen wir mal die Gewindedurchmesser M 4, M 5 und M 6: 4 × 6 = 24. Die Wurzel aus 24 ist etwas kleiner als die aus 25, also irgendwas mit Vier Komma Hugo. Natürlich wäre „Emm Vier Komma Hugo“ ein saublöder Gewindedurchmesser. Also rundet man und nimmt 5 mm. Und richtig: zwischen M 4 und M 6 findet sich die Größe M 5.
Was haben Normzahlen mit Fesselballons zu tun?
Die in der DIN 323 und der ISO 3 festgelegten Normzahlreihen heißen auch Renard-Serien oder Renard-Reihen. Sie gehen nämlich auf einen gewissen Charles Renard (1847-1905) zurück, einen französischen Militäringenieur. Der konstruierte unter anderem ein Luftschiff und eine Art Road Train aus einer Zugmaschine und mehreren angetriebenen und gelenkten Anhängern, den Train Renard. Und er machte sich Gedanken über die Stärken von Halteseilen für Fesselballons. Mit seinem geometrisch abgestuften System benötigte man nur noch 17 verschiedene Stärken der Seile. Vorher waren es 425 gewesen.
Die nach DIN und ISO genormten Renard-Serien, die Normzahlreihen benutzen als Faktoren Wurzeln der Zahl Zehn und beginnen alle mit der Eins. Aufhören tun sie mit der Zehn. Das heißt, sie hören nicht wirklich auf, denn man kann sie ja mit den Faktoren 10, 100, 1000 usw. im Prinzip beliebig fortführen. Das sieht man zum Beispiel an der Tabelle mit den metrischen Spitzgewinden weiter oben: oberhalb von M 10 geht es – mit etwas gutem Willen gesehen – mit den zehnfachen Maßen der Gewinde bis M 10 weiter. Vermutlich basieren diese Gewindedurchmesser also auf irgendwelchen Normzahlen.
Die genormten Renard-Serien
Die Normzahlenreihen, die Renard-Serien nach DIN 323 basieren auf Wurzeln der Zahl Zehn. Sie beginnen wie gesagt alle mit der Eins und hören mit der Zehn auf. Um diesen Bereich geometrisch aufzuteilen benutzt man als Faktor jeweils Wurzeln der Zahl Zehn. Will man fünf Stufen haben, benutzt man die fünfte Wurzel aus Zehn, für zehn Stufen die zehnte, für zwanzig Stufen die zwanzigste und für vierzig Stufen die vierzigste. So ergeben sich die vier Normzahlenreihen R5, R10, R20 und R40. die tatsächlichen Werte der Normzahlen, die in der Tabelle zu finden sind, sind ein klein wenig gerundet, damit sie ein wenig handlicher werden.
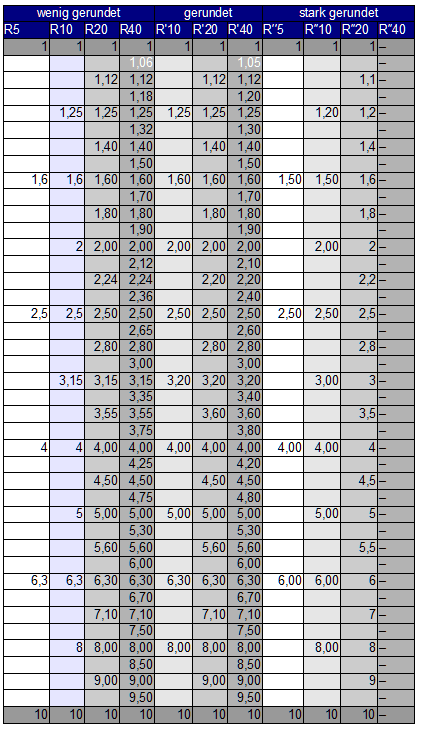
Es gibt nun noch die R‘- und R“-Reihen. Die mit dem einen Strich sind stärker gerundet als die ohne Strich. Und die mit zwei Strichen sind noch etwas stärker gerundet. Außerdem kann man auch hergehen und aus einer der Reihen nur jede soundsovielte Zahl nehmen. Dazu gibt man dann mit einem Schrägstrich hinter dem Namen der Reihe an, jede wievielte Zahl verwendet werden soll. Außerdem schreibt man in Klammern dahinter, von welcher bis zu welcher Zahl die Reihe reichen soll: R“20/2 (1..20) wäre dann jede zweite Zahl aus der Reihe R“20 von 1 bis 20: 1; 1,2; 1,6; 2; 2,5; 3; 4; 5; 6; 8; 10; 12; 16; 20; . Na, kommt uns das nicht bekannt vor? Na klar doch: Das sind die Durchmesser der metrischen Spitzgewinde von M 1 bis M 20.
Achso, noch was: Nein! Die Normzahlen haben nichts mit dem very britishen Zoll zu tun, auch wenn öfter mal 2,5 vorkommt…
1 Pingback