Physikalische Einheiten und wie sie zusammenhängen II

Physikalische Einheiten und der Formelkram

Grundlegende physikalische Einheiten sind für sich selbst definiert. Sie reichen aber lange nicht aus, um alle Größen anzugeben, die in der Physik vorkommen. Die vielen Einheiten, die man braucht, um physikalische Vorgänge zahlenmäßig zu beschreiben, werden jedoch allesamt aus den Grundeinheiten zusammengebaut.

Das ist der zweite Teil einer mehrteiligen Geschichte. Zum ersten Teil geht es hier.

Ein einfaches Beispiel für eine zusammengesetzte Einheit ist die der Geschwindigkeit: m/s. Meter pro Sekunde. Geschwindigkeit ist jetzt nichts anderes, als dass Verhältnis zwischen dem Weg, den man zurückgelegt hat und der Zeit, die man dafür gebraucht hat. Man sagt „Meter pro Sekunde“ könnte aber „m/s“ auch als „Meter geteilt durch Sekunde“ lesen. Und man könnte es auch als Bruch mit Meter im Zähler und Sekunde im Nenner auffassen.

Na sowas! Drei verschiedene Dinge – ein Name? Nun, der Physikalische Einheiten- und Formelkram in der Physik ist nun mal angewandte Mathematik. Und in der Mathematik wird einem öfter mal das Gleiche unter verschiedenen Namen verkauft. Ein Verhältnis ist nichts anderes als ein Bruch. Und ein Bruch nichts anderes als eine Division, also eine Geteilt-Durch-Aufgabe. Drei Namen für ein und dasselbe Ding: Anstelle des altmodischen Doppelpunkts für „Geteilt-Durch“ – m:s – kann man auch einen Schrägstrich schreiben: m/s. Und dieser Schrägstrich ist exakt das gleiche wie der schräge Bruchstrich aus Uromas Schulzeit. Und auch nichts anderes, als der waagrechte, den man heute macht.

Hier kommt jetzt auch das Geheimnis für Leute, die in Physik keine Formeln büffeln und trotzdem immer die richtige Formel wissen wollen: Die Formel versteckt sich nämlich in der Einheit. Wer die Einheit kennt, kennt die Formel. Und wenn die Einheit einen eigenen Namen hat, muss man halt noch wissen, wie die Einheit aussieht, wenn man sie aus Grundeinheiten zusammengesetzt schreibt.

Geschwindigkeit misst man in m/s oder km/h. Beide Male steht der Weg (m bzw km) im Zähler, die Zeit (s, h) im Nenner. Also muss man den Weg durch die Zeit teilen: Geschwindigkeit ist Weg geteilt durch Zeit.

Für die Geschwindigkeit in m/s oder km/h gibt es keine eigenen Einheitennamen. In der Seefahrt gibt es aber die Geschwindigkeitseinheit Knoten. Knoten sind nichts anderes, als Seemeilen pro Stunde: sm/h. Das „pro“ ist nichts anderes als ein Bruchstrich und nichts anderes als ein Geteilt-Durch-Zeichen. Die zurückgelegten Seemeilen stehen davor, die benötigte Zeit dahinter. Also muss man die Seemeilen durch die Zeit teilen. Also auch wieder Strecke durch Zeit.So einfach ist das.

Weg, Zeit und Geschwindigkeit

Gerade haben wir gesehen, dass man die Geschwindigkeit bekommt, wenn man den Weg durch die Zeit teilt. Für den Weg schreibt man s, für die Zeit t und für die Geschwindigkeit v. Die Meter sind der Weg s, die Sekunden die Zeit t. Also wird aus der Einheit m/s die rechte Seite der Formel Formel v = s/t. Oder mit waagerechten Bruchstrich geschrieben:

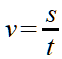
Ein Beispiel: Wer eine Jägerprüfung machen will, muss dabei auf den sogenannten laufenden Keiler schießen. Das ist eine Pappendeckel-Wildsau, die von einer Maschine über eine Schneise von 6 m Breite gezogen wird. Und zwar in 2 Sekunden. Wie schnell ist die Sau also in Meter pro Sekunde?

Solche Aufgaben löst man nach dem bewährten Schema “ Gegeben – Gesucht – Formel – Werte einsetzen – Ausrechnen“:

Geg.: s = 6 m; t = 2 s

Ges.: v

Lsg.:

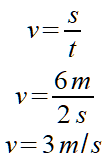
Ganz wichtig dabei ist, dass du die Einheiten mitziehst: Die Sechs von den Metern teilst du durch Zwei von den Sekunden und das ergibt natürlich drei. Das ist der Zahlenwert. Wenn du nun die Meter durch die Sekunden teilst bekommst du die Einheit des Ergebnisses m/s. Und wenn die stimmt, Geschwindigkeit soll ja in Meter pro Sekunde herauskommen, stimmt höchstwahrscheinlich auch deine Formel. Wenn die Einheit nicht stimmt, dann ist aber auf jeden Fall was mit der Formel faul. Physikalische Einheiten also immer mitziehen beim Ausrechnen!

Physikalische Einheiten und Formeln verstehen

Sich die Formel aus der Einheit abzuleiten, ist ja schon mal was. Noch besser ist es aber, wenn man sich klarmacht, warum die Formel so und nicht anders aussieht. Das ist im Grunde sehr einfach. Man muss sich nur überlegen, welche der Ausgangsgrößen – hier also Weg und Zeit – was mit dem Ergebnis macht. Alles, was das Ergebnis größer macht, muss im Zähler stehen. Und alles, was das Ergebnis kleiner macht, gehört in den Nenner.

Legt man in der gleichen Zeit einen größeren Weg zurück, muss man schneller gewesen sein. Der Weg macht das Ergebnis also größer und gehört daher in den Zähler. Braucht man für den gleichen Weg aber mehr Zeit, war man langsamer. Die Zeit macht das Ergebnis kleiner und gehört deswegen in den Nenner.

Diese Regel stimmt immer. Bei komplizierteren Formeln kann es nun sein, dass man eine der Ausgangsgrößen quadrieren oder sonst was muss oder vielleicht noch ein Faktor dazu gehört. Aber, egal, was man mit der Größe anstellt, wenn sie das Ergebnis größer werden lässt, gehört sie in den Zähler. Und wenn sie das Ergebnis kleiner werden lässt, gehört sie in den Nenner.

Wenn du dir klargemacht hast, dass der Weg die Geschwindigkeit größer macht und deswegen in den Zähler gehört und die Zeit die Geschwindigkeit kleiner macht und deswegen in den Nenner gehört, wirst du bei dieser Formel nie wieder Zähler und Nenner verwechseln. Oder anders ausgedrückt: Du wirst die Formel nicht vergessen, wenn du den Vorgang verstanden hast, den sie beschreibt.

Geschwindigkeit und Beschleunigung

Gerade haben wir gesehen, dass die Geschwindigkeit das Verhältnis zwischen zurückgelegten Weg und benötigter Zeit ist. Wenn du mit deinem Auto – um eine einfache Zahl zu nehmen – 72 km/h schnell fährst, sind das 20 m/s. Weil 1 km 1000 m hat und 1 Stunde 3600 Sekunden, sind die km/h immer 3,6 mal so viel wie die m/s. In der Fahrschule wird das ganz grob auf vier gerundet: Wenn man 100 km/h fährt, legt man, so wird dort gerechnet, in jeder Sekunde etwa 25 m zurück, die man für die Reaktionszeit zum Bremsweg hinzufügen muss, um den Anhalteweg zu bekommen.

Geschwindigkeiten ändern sich aber in der Praxis auch. Um 72 km/h bzw. 20 m/s schnell zu fahren, muss man das Auto zunächst beschleunigen. Man kann das nun mit viel Gas tun oder mit wenig. Mit viel Gas hat man die Geschwindigkeit in kürzerer Zeit erreicht als mit wenig.

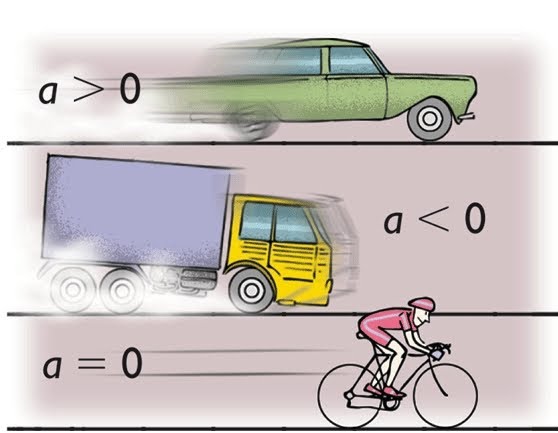
Das eine Mal hat man stärker beschleunigt, das andere Mal weniger stark. Die Beschleunigung ist die Geschwindigkeitsänderung pro Zeiteinheit. Nehmen wir an, du hast dein Auto gleichmäßig in 10 Sekunden aus dem Stand auf die 72 km/h oder 20 m/s beschleunigt. Dann bist du dabei in jeder Sekunde um 2 m/s schneller geworden. Als Rechenaufgabe geschrieben sieht das so aus:

Geg.: Δv = 20 km/h; t = 10 s

Ges.: a

Lsg.:

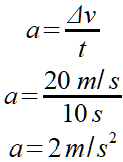
Das kleine a ist das Formelzeichen für die Beschleunigung, die hier 2 m/s² beträgt. Dass hier jetzt auf einmal dieses seltsame Δ vor dem v für die Geschwindigkeit steht, muss uns nicht stören. In der Physik schreibt man immer dieses Delta vor die Einheit, wenn es darum geht dass diese Größe sich ändert. Die Änderung einer Größe hat natürlich die gleiche Einheit wie die Größe selbst und man rechnet auch genauso mit ihr. In unserem Beispiel haben wir das Auto aus dem Stand in 10 Sekunden auf die 20 m/s beschleunigt. Die Beschleunigung wäre aber die gleiche gewesen, wenn wir es von 20 m/s auf 40 m/s beschleunigt hätten. Oder von jeder beliebigen anderen Geschwindigkeit aus um 20 m/s. Es kommt auf den Geschwindigkeitsunterschied an und deswegen eben die Unterscheidung mit dem davor gestellten Delta.

Bei dieser Rechnung haben wir auch wieder treu und brav die physikalischen Einheiten mitgeschleppt. Und deswegen haben wir auch im Ergebnis diese seltsameEinheit m/s², Meter pro Quadratssekunde, herausbekommen. Die stimmt tatsächlich, auch wenn einem Quadratssekunden etwas komisch vorkommen. Physikalische Einheiten halt…

Sie entsteht ganz einfach deswegen, weil wir hier im Endeffekt zweimal durch Sekunden geteilt haben: Einmal für die Geschwindigkeit und ein weiteres Mal für die Beschleunigung. Man kann das auch an der Berechnung nachvollziehen: Im Zähler steht ja m/s. D.h. es wird durch die Sekunden geteilt. Die Sekunden aus den m/s kann man daher unter den Bruchstrich ziehen. Das ändert nichts, weil dann genauso durch sie geteilt wird. Im Nenner steht nun bereits die Zeit, die man für die Geschwindigkeitsänderung braucht, ebenfalls als s. Deswegen ergibt das Sekunde mal Sekunde oder Sekunde hoch zwei: s². Und dazu kann man auch Sekunde zum Quadrat oder Quadratsekunde sagen.

Beschleunigung und Kraft: Das Newton

Um dein Auto in 10 Sekunden von null auf 72 km/h bzw. 20 m/s zu beschleunigen, hat es eine bestimmte Kraft gebraucht. Diese Kraft haben deine Antriebsräder auf den Asphalt gebracht und damit dein Auto nach vorne geschoben.

Nehmen wir an, das Auto hat eine Masse von 1500 kg. Aus dieser Masse und den ebenfalls gegebenen 2 m/s ² für die Beschleunigung kann man diese Kraft berechnen. Stellen wir also wieder unsere grundlegende Überlegung an: Die Kraft, die ich zum Beschleunigen brauche wird umso größer, je stärker ich beschleunige. Und sie wird ebenfalls umso größer, je größer die Masse ist, die ich beschleunige. Beide Werte machen also das Ergebnis größer und deswegen müssen auch beide in den Zähler:

F = m * a

Kraft = Masse mal Beschleunigung. Hier gibt es zwar keinen Nenner, aber man kann sich in so einem Fall jederzeit vorstellen, dass der Nenner ganz einfach Eins ist. Der Wert einer Zahl ändert sich ja nicht, wenn ich sie in den Zähler setze und eine Eins in den Nenner schreibe. Das ist ja nichts anderes als das Teilen durch eins: 3/1 = 3, 5/1 = 5, 9/1 = 9 usw. Wenn dir das hilft, kannst du dir also jederzeit, wenn in einer Formel keinen Nenner ist, einen solchen vorstellen, der eben eine Eins enthält.

Machen wir also aus dem Beispiel eine Aufgabe:

Geg.: m = 1500 kg; a = 2 m/s²

Ges: F

Lsg.:

F = m * a

F = 1500 kg * 2 m/s²

F = 3000 kgm/s²

F = 3000 N

Kurznamen für Physikalische Einheiten aufgedröselt

Die Einheit der Kraft ist eigentlich kgm/s². Es gibt aber dafür sozusagen den Kurznamen Newton, nach dem britischen Physiker Isaac Newton (1642 – 1726). Wie war das noch mal? In der Einheit steckt die Formel! Manchmal sieht man das genau wie bei km/h oder m/s, manchmal nicht, wie beim Newton (N), der Einheit der Kraft. Schaut man jedoch genauer hin, sieht man, dass ein Newton nichts anderes ist als 1 kgm/s². „Newton“ sagt sich halt schneller als „Kilogrammmeter pro Quadratsekunde“. Ähnlich ist es mit dem Watt und dem Joule. Aber da kommen wir noch drauf.

Wer aber weiß, dass ein Newton eigentlich gleich einem kgm/s² ist, kann sich daraus die Formel für die Kraft aus Masse und Beschleunigung heraus puhlen: Die Kilogramm sind natürlich die Masse m. Bleibt m/s² – und das ist die Einheit der Beschleunigung a. Also ist die Kraft Masse mal Beschleunigung

F = m * a

Aus der Definition

1 N = 1kgm/s²

geht hervor, dass 1 N diejenige Kraft ist, die man benötigt, um einen Körper mit einer Masse von 1 kg mit 1 m/s ² zu beschleunigen. Wenn man also einen solchen Körper mit einem Newton stetig anschiebt, wird er in jeder Sekunde um 1 m/s schneller.

Weg, Zeit, Beschleunigung, Kraft… Weiter geht es mit Arbeit, Energie und Leistung – und zwar hier!