Wie eine Tonleiter entsteht
Musik beruht – zumindest zu einem großen Teil – letztendlich auf Physik. Welche Töne zusammen gut klingen und welche grün, kann man physikalisch herleiten. Im ersten Teil dieses Blogartikels war von Schwingungen, Frequenzen, Grund- und Obertönen die Rede. Pythagoras war nach unserem Wissen der erste, der sich mit den Längenverhältnissen von schwingenden Saiten befasste. Also mit Frequenzverhältnissen. Damit begründete er die Musiktheorie, die Harmonielehre. Dabei fand er, das zwei Töne umso besser zusammenklingen, je einfacher das Verhältnis ihrer Frequenzen zueinander ist. Und außerdem erfand er eine Methode, um eine Tonleiter zu bauen.
Dies ist der zweite Teil eines zweiteiligen Artikel. Zum ersten Teil geht es hier.
Pythagoras konnte an seinem Monochord ja sehr gut verschiedene Saitenlängen und damit Frequenzen einstellen und vergleichen. Mit dem Verhältnis 3/2 bekommt man ja, wie wir gesehen haben, die Quinte. Das Verhältnis 4/3 ergibt eine Quarte. 5/4 ergibt eine große Terz und 6/5 eine kleine. Die letzeren spielen aber beim Aufbau einer Tonleiter zunächst keine Rolle, denn die baute Pythaoras mithilfe von Quinten. Die Aufgabe bestand sozusagen darin, zwischen einem Ton und seiner Oktave Zwischenstufen einzuziehen, damit man einen Tonvorrat zum Musizieren bekommt.
Eine Tonleiter aus Quinten
Pythagoras ging nun her und nahm zu einem Grundton die Quinte. Damit hatte er zwischen dem Grundton und der Oktave schon einmal einen weiteren Ton eingebaut. Darauf setzte er nun noch mal eine Quinte, die nun aber über der Oktave lag. Macht nichts: Man kann die Frequenz ja halbieren und damit den Ton um eine Oktave erniedrigen. So liegt er wieder innerhalb der Oktave über dem Grundton. Und man hat einen weiteren Ton in seiner Tonleiter.
Das trieb der alte Grieche so lange weiter, bis er nach zwölf Schritten bei der Oktave seines Grundtons angelangt. Damit hatte er die Oktave in zwölf Stufen unterteilt, die man heute Halbtöne nennt. Und damit war eigentlich das Grundgerüst der abendländischen Musik geschaffen. Aus den zwölf Halbtönen kann man nun die für eine bestimmte Tonleiter notwendigen Töne auswählen.
Basis für Frequenzen und Harmonie: Der Kammerton
In der Tabelle hier sieht man die Frequenzen der Töne in einer chromatischen – das bedeutet alle (Halb-)Töne zusammen in einer Skala – Tonleiter , die man nach der Methode von Pythagoras über dem Kammerton A mit 440 Hz zusammengeschraubt hat. Das ist – siehe oben – das eingestrichene A, das a‘. Das ist der sogenannte Kammerton, auf denen sich eigentlich die ganze Musik aufbauen sollte.
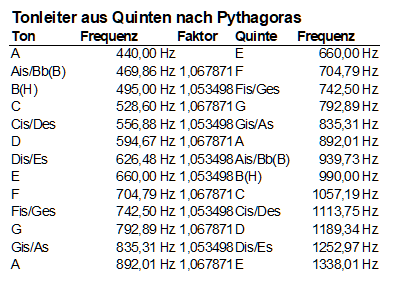
Diese 440 Hz, die ich hier zugrundegelegt habe, sind nach DIN und ISO genormt. Das hat allerdings nichts daran geändert, dass sich seit weit mehr als einem Jahrhundert die Musiker herum streiten, welche Frequenz dieser Ton haben sollte.
Tatsächlich stimmen in Deutschland und Österreich die Orchester mit konstanter Bosheit ihre Instrumente mit 443 Hz und in der Schweiz mit 442. Außerdem gibt es Leute, die für etwas tiefere Frequenzen plädieren. Musiker haben da Argumente, die auf technische Eigenschaften bestimmter Musikinstrumente abheben bzw. auf die obere Grenze des Stimmumfangs von Sopranistinnen.
Ich fand sogar eine Verschwörungstheorie zu diesem Thema: Man habe diesen Kammerton seinerzeit, 1932, böswillig angehoben, um damit die Menschen zu manipulieren. Der alte Kammerton lag nämlich bei 432 Hz. DNS und Alphawellen würden angeblich auf einer Oktave dieser alte Frequenz schwingen.

Ich habe nachgeguckt und herausgefunden, dass die Frequenz der Alphawellen zwischen 8 und 13 Hz beträgt. Geht man von 440 Hz fünf Oktaven hinunter, bekommt man für dieses bereits unter der Hörschwelle liegende A einem Frequenz von 13,75 Hz. Legt man 432 Hz zugrunde, landet man bei 13,5 Hz. Gegenüber einer Bandbreite von 8 Hz bis 13 Hz der Alphawellen dürften diese 0,25 Hz Unterschied wohl kaum eine Rolle spielen.
Interessant zu wissen ist auch, was auf dieser Website, wo ich die Geschichte mit dem angeblich böswillig erhöhten Kammerton fand, für teuer Geld verkauft wird: esoterische Wasserfilter, Strahlenschutz, Vitalschmuck und derlei Artikelchen mehr. So, so. Naja: Ein jeder möge seine eigenes Hirn benutzen…
Exkurs: B oder H?
In der Tabelle mit den Tönen und den Quinten aus denen sie entstehen ist ein Ton mit „B(H)“ bezeichnet. Das kommt daher, dass dieser Ton ein Kind mit zwei Namen ist. Und zwar heißt er (unter anderem) im deutschen Sprachraum H. Das ist unlogisch, denn im Alphabet kommt nach dem A eben das B. Und so heißt dieser Ton im angelsächsischen Sprachraum auch B.

Der komische Name H hat sich bei uns im Mittelalter eingeschlichen. Es ist natürlich nahe liegend, anzunehmen, dass da jemand ein kleines b mit einem kleinen h verwechselt hat. Tatsächlich war es aber nicht ganz so einfach. Es ist relativ kompliziert und hat damit zu tun, dass man in der mittelalterlichen Kirchenmusik sozusagen zwei verschiedene bs kannte und dass eine mit einem rundlichen b und das andere mit einem dem h ähnelnden eckigen b schrieb.
Wenn man lediglich Noten auf Notenlinien liest, spielt es ja keine Rolle wie Töne heißen. Man muss lediglich wissen, wie man sie spielt oder singt. Außer einzelnen Tönen gibt es aber auch Akkorde. Die kann man natürlich mit ihren Noten auf Notenlinien schreiben. Zum Beispiel für Klavier. Öfter aber – zum Beispiel für Gitarrengriffe – schreibt man Akkorde auch mit Akkordsymbolen. Und das sind Buchstaben, nämlich jeweils der Name des Grundtons.
Ich persönlich nenne das H lieber B. Dass das logischer ist, ist eigentlich der weniger wichtige Grund. Wichtiger ist, dass ich ein Blues- und Rockmusiker bin. Blues und Rock kommen aus dem angelsächsischen Sprachraum. Und Songbooks und dergleichen dafür natürlich oft auch. Wenn man sich im Netz Gitarrenbegleitungen zu solchen Songs sucht, stammen die oft auch aus dem angelsächsischen Sprachraum. Deswegen muss man eben wissen, dass unser H dort B heißt.
Die Wolfsquinte und das pythagoräische Komma
Nun gab es aber bei der Geschichte mit der Tonleiter aus Quinten ein übles Problem. Eine Oktave bedeutet ja eine Verdoppelung der Tonhöhe, also der Frequenz. Das nächste A über dem Kammerton sollte also 880 Hz haben. Schauen wir uns die Tabelle mit den Tönen an, die sich so ergeben, stellen wir fest, dass sie nicht hinhaut. Wir landen nämlich mit unseren Quintenschritten am Schluss bei 892,01 Hz. Diesen Unterschied nennt man das pythagoräische Komma.

Würde man das Bestimmen der Tonleitertöne mit den Quinten so fortführen, bekämen wir bei jeder Oktave einen größeren Fehler. Also blieb man dabei, dass die nächste Oktave immer die doppelte Frequenz hat. Dadurch wurde aber die letzte Quinte verkürzt und das hatte üble Folgen.
Ein einfaches Frequenzverhältnis ergibt einen harmonischen Klang. Verändert man ein einfaches Verhältnis wie zwei zu drei ein wenig, kommt automatisch ein sehr krummes Verhältnis heraus: nämlich etwa 37/25 bei der letzten Quinte. Und wenn ein einfaches Frequenzverhältnis einen harmonischen Klang gibt, ergibt ein kompliziertes einen disharmonischen.
Tatsächlich klingt diese letzte Quinte in der Tonleiter des alten Pythagoras grauenhaft. Irgendjemand muss wohl mal gefunden haben, dass sie wie ein Wolf heult. Oder dass sie der Feind des Musikers ist, wie man den Wolf ja früher auch als Feind des Menschen betrachtet hat. Jedenfalls nennt man sie Wolfsquinte oder Quintenwolf.
Bachs Tonleiter: Die temperierte Stimmung
Diese Wolfsquinte ärgerte die Musiker viele Jahrhunderte lang. Johann Sebastian Bach, der große Barockmusiker entwickelte nun eine Tonreihe, welche diese Wolfsquinte vermied. Im Prinzip ging es darum, das pythagoräische Komma sozusagen zu verteilen. Eine solche Bastelei an den Tönen bezeichnet man als Temperieren.

Die Stimmung der Töne wie sie Bach vornahm, bezeichnet man als wohltemperierte Stimmung. Das bekannte Wohltemperierte Klavier von Johann Sebastian Bach ist eine Sammlung von je einem Präludium und einer Fuge in jeder der zwölf Tonarten. Bach schrieb diese Stücke sozusagen als Demo für seine Stimmung. Sie zeigen nämlich, dass diese wohltemperierte Stimmung in allen zwölf Tonarten funktioniert.
Frequenzen und Harmonie bei der gleichstufigen Stimmung
Heute stimmt man in der Regel noch etwas anders. Eigentlich ist die sogenannte gleichstufige Stimmung, die wir heute verwenden, sehr nahe liegend. Schaut man sich mal eine Reihe von Tönen an, von denen jeder eine Oktave höher ist, stellt man fest, dass der absolute Abstand der Frequenzen immer größer wird: 110 Hz, 220 Hz, 440 Hz, 880 Hz, 1760 Hz… Was gleich bleibt, ist der Faktor. Bei der Oktave beträgt er Zwei. Das gleiche ist natürlich auch bei der Quinte der Fall, hier ist der Faktor eben 3/2 oder 1,5.
Zahlenfolgen, bei denen jede Zahl um einen bestimmten Faktor größer ist als die vorhergehende, bezeichnet man als geometrische Reihen. Wenn von Oktave zu Oktave die Abstände der Frequenzen absolut immer größer werden, muss das im Grunde auch von Halbton zu Halbton so sein. Baut man die zwölf Haltertöne einer Oktave mit der Quinten-Methode, stimmt das aber nicht so ganz. Man sieht das auch in der Tabelle oben.
Das Problem löst sich, wenn man sich überlegt, welchen Faktor man nehmen muss, wenn man nach zwölf mal Multiplizieren genau auf Zwei kommen will. Und das ist die zwölfte Wurzel aus zwei. Multipliziert man eine Zahl zwölf mal mit dieser zwölften Wurzel aus zwei, kommt genau das Doppelte dieser Zahl heraus. Im Falle der Frequenz eines Tones also der gleiche Ton eine Oktave höher.

Die zwölfte Wurzel aus Zwei liegt etwa bei 1,06. Damit liegt sie ungefähr in der Mitte zwischen den beiden Faktoren, die sich beim Aufbau der Tonleiter mit den Quinten ergeben.
Natürlich beißt sich das jetzt wieder mit dem genauen Verhältnis 2/3 der Quinte. Aber diese Abweichung ist so gering, dass man damit gut leben kann. Und deswegen wird heute allgemein diese gleichstufige Stimmung angewendet.
Die Oktave in Dur und Moll: Die Stammtöne
In der Regel verwendet man in einem Musikstück nicht alle zwölf Halbtöne einer Oktave. Man nimmt immer gewissermaßen eine Auswahl, die man dann Tonleiter nennt. Man benutzt immer sieben Töne aus einer Oktave und der nächste Ton ist dann wieder der Grundton um eine Oktave höher. Das sind insgesamt acht Töne und daher kommt auch der Ausdruck Oktave.
Schaut man sich nun mal eine C-Dur-Tonleiter an, besteht diese aus den Tönen C,D,E,F,G,A und B(H). Der achte Ton ist dann wieder ein C. Wie man hier im Bild sieht, sitzen diese Töne alle entweder auf Linien des Notensystems oder in Zwischenräumen zwischen diesen Linien. Normalerweise sitzen auf den Notenlinien und in den Zwischenräumen immer ganze Töne. Das ist aber nicht ganz wahr.
Was man nicht sie, ist das folgende: Der Abstand zwischen dem E und dem F ist seltsamerweise kein ganzer Ton, sondern nur ein halber. Und auch vom B zum C ist es nur ein solcher Halbton. Dadurch ergibt sich, wenn man die Töne von einem C zum nächsten spielt, eine Tonleiter, bei der zwischen dem dritten und dem vierten sowie dem siebenten und dem achten Schritt kein Ganzton- sondern nur ein Halbtonschritt ist.

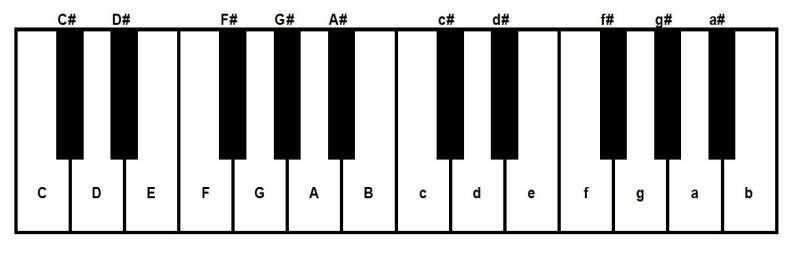
Eine solche Tonleiter heißt C-Dur- Tonleiter und ist auf dem Klavier ganz einfach zu spielen. Man benötigt nämlich dafür nur weiße Tasten. Auf der weiter oben abgebildeten Klaviertastatur sieht man, dass an bestimmten Stellen keine schwarze Taste zwischen zwei weißen Tasten ist. Das sind diese Halbtonschritte zwischen dem E und dem F sowie dem B und dem C.
Deswegen findet man auf jeder solchen Tastatur, also auch bei einem Keyboard oder einer Orgel, das C ganz leicht: Es ist immer die weiße Taste links von der ersten der zwei schwarzen Tasten. Und die weiße Taste neben der ersten der drei schwarzen Tasten ist immer ein F.
Diese Töne, die zusammen eine (C-)Dur-Tonleiter bilden, die nur die weißen Tasten braucht, heißen Stammtöne. Auf einem Notensystem liegen sie alle auf Linien oder in Zwischenräumen.

Übrigens kann man diese Töne auch spielen, wenn man mit dem A anfängt. Dann sitzen die Halbtonschritte auf einmal zwischen dem zweiten und dem dritten sowie dem sechsten und dem siebten Schritt. Eine solche Tonleiter nennt man Moll-Tonleiter. In diesem Fall A-Moll. Genauer gesagt ist das das sogenannte natürliche Moll. Dur und (natürliches) Moll sind die beiden Tongeschlechter, die man hauptsächlich verwendet. Durus bedeutet hart und Mollus bedeutet weich. Dur ist eher lustig, Moll eher ein bisschen traurig. Dur ist männlich, Moll ist weiblich. Und wenn man es mit der alten chinesischen Philosophie erhält: Dur ist Yang und Moll ist Yin…
Die Vorzeichen
Wenn man Dur- bzw. Moll-Tonleitern auf anderen Tönen aufbauen will, benötigt man die schwarzen Tasten auf dem Klavier und bei den Noten muss man Vorzeichen, Kreuze (#) und Bes (b) verwenden. Nur so kriegt man die Halbtonschritte wieder an die richtigen Stellen für Dur bzw. Moll. Ein Kreuz besagt, dass der Ton einen halben Ton höher spielen muss und ein B sagt, dass man ihn einen halben Ton tiefer spielt. Auf dem Klavier ist das die schwarze Taste links von der weißen bzw. rechts von der weißen.

Der Halbton über einem Ton bekommt ein -is an den Namen angehängt: Cis, Dis, Fis, Gis, Ais. Und der Halbton unter einem Ton erhält ein -es: Des, Es, Ges und As. Der unter dem H ist ein Sonderfall: Bei uns heißt er B und im angelsächsischen Sprachraum „B flat“ (Bb), weil das B dort ja unser H ist. Dort hängt man auch an die erhöhten Töne das Wörtchen „sharp“ an und an die erniedrigten ein „flat“. Schreiben tut man sie C#, D#… und Db, Eb usw.
Enharmonische Verwechselungen
Der Halbton zwischen dem C und dem D kann nun Cis heißen, aber auch Des. Und der zwischen F und G heißt Fis oder Ges. Das nennnt man enharmaonische Verwechselungen. Aber: Wie blöd ist das denn? Zwei Namen für das gleiche Kind?
Tatsächlich hat die Möglichkeit, den gleichen Ton verschieden zu benennen ihren guten Grund. Würde man die Kreuze und Bes vor jede einzelne Note machen (wie im Bild weiter oben), wäre es in der Tat egal. Aber man schreibt die Kreuze und Bes immer nur an den Anfang der Notenzeile. Und der Musiker muss sie sich dann für jede Note, die auf der jeweiligen Linie bzw. in dem Zwischenraum steht, selbst denken. Und auch noch in den Oktaven drüber und drunter: Im untersten Zwischenraum ist ja auch ein F bzw. in diesem Fall, bei G-Dur ein Fis.
Das wird in der Abbildung der G-Dur-Tonleiter klar. Der eine Halbtonschritt liegt zwischen dem B und dem C. Das ist wie bei C-Dur kein Problem. Der andere aber ist zwischen dem Fis und dem G. Da nun kein F in dieser Tonleiter vorkommt, ist ganz einfach jeder Ton auf der obersten Linie kein F sondern ein Fis.

Mit einem Be über der obersten Linie, also einem Ges, würde das nicht funktionieren: Das G kommt ja in der G-Dur-Tonleiter auch vor. Und deswegen wüsste man dann nie, ob eine Note über der obersten Linie ein G oder ein ges sein soll.
Das soll nun für diesen Artikel genug Harmonielehre sein. Wenn man hier jetzt weitermachen will, hilft ein Notensatzprogramm ungemein. Ein solches – natürlich kostenloses – möchte ich demnächst nämlich hier vorstellen. Daher auch dieser theoretische Artikel. Damit sich auch absolute Musik-Noobs hier einlesen und dann gleich mitexperimentieren können.

2 Pingbacks